Vecto Trong Không Gian Oxyz

Vecto trong không gian lớp 11 luôn là một dạng toán khó đòi hỏi các em học sinh phải hiểu sâu, nắm vững kiến thức mới có thể hiểu bài và đạt được điểm cao. Để thực sự hiểu rõ kiến thức về dạng toán này, hãy cùng VUIHOC ôn tập lại toàn bộ lý thuyết và luyện giải các dạng bài tập nhé!

Bài tập trắc nghiệm vectơ trong không gian lớp 11 (có đáp án)

4 điểm A, B, C, D không thẳng hàng trong không gian O. Khi nào A, B, C, D có đầy đủ điều kiện để cấu thành nên hình bình hành?

S. ABCD, vecto SA= vecto a, vecto SB= vecto b, vecto SC= vecto c, vecto SD = vecto d

A. Vecto a +vectp c = Vecto b + Vecto d

B. Vecto a + Vecto b = Vecto c + Vecto d

C. Vecto a + Vecto d = Vecto b + Vecto c

D. Vecto a + Vecto b + Vecto c + Vecto d

Cho tứ diện ABCD, định nghĩa G là trọng tâm tứ diện ABCD khi:

$\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}+\overrightarrow{GD}=\overrightarrow{0}$

Khi đó khẳng định nào dưới đây là sai?

A. Trung điểm của IJ với I là trung điểm của AB và J là trung điểm của CD, giao nhau là G.

B. Đoạn thẳng nối trung điểm của AC và BD là G.

C. Trung điểm của AC và BD là G.

Câu 7: Ba vecto $\overrightarrow{a}, \overrightarrow{b}, \overrightarrow{c}$, không đồng phẳng nếu?

A. Ba đường thẳng chứa vecto không cùng 1 mặt phẳng

B. Ba đường thẳng chứa chúng thuộc cùng 1 mặt phẳng

C. Ba đường thẳng chứa không cùng song song một mặt phẳng

D. Ba đường thẳng chứa vecto không cùng song song một mặt phẳng

Có tứ diện ABCD với trung điểm AB và CD là trung điểm của E và E. Có AB = 2a, CD = 2b, EF = 2c. M là điểm bất kỳ. Vậy MA2+MB2 là

Tọa độ điểm và vector trong không gian là những dạng toán quan trọng trong chương trình toán học THPT. Vì vậy bài giảng video dưới đây thầy Phạm Anh Tài sẽ cung cấp cho các em đầy đủ kiến thức về phần hình oxyz - Tọa độ điểm và vector, giải một số vì dụ và bài tập một cách chi tiết và dễ hiểu nhất để các em tự tin khi gặp dạng bài này.

Đăng ký ngay để được thầy cô tổng hợp kiến thức và xây dựng lộ trình ôn thi sớm đạt 9+ ngay từ bây giờ

Trên đây toàn bộ kiến thức về vecto trong không gian thuộc chương trình Toán lớp 11 mà VUIHOC chia sẻ với các bạn học sinh. Hy vọng rằng, sau bài viết này, các em học sinh đã có thể nắm vững kiến thức về dạng bài vecto trong không gian và luyện tập một cách thuần thục. Để có thêm các thông tin bổ ích, các em hãy truy cập Vuihoc.vn nhé!

⭐Bộ Sách Thần Tốc Luyện Đề Toán - Lý - Hóa THPT Có Giải Chi Tiết

Phép chiếu song song. Hình biểu diễn của một hình không gian

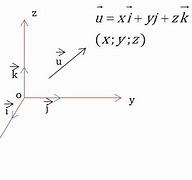
Cho hai vectơ \(\overrightarrow a  = ({a_1};{a_2};{a_3})\), \(\overrightarrow b  = ({b_1};{b_2};{b_3})\).

a) Biểu diễn từng vectơ \(\overrightarrow a \) và \(\overrightarrow b \) theo ba vectơ \(\overrightarrow i ,\overrightarrow j ,\overrightarrow k \)

b) Tính các tích vô hướng \({\overrightarrow i ^2},{\overrightarrow j ^2},{\overrightarrow k ^2}\), \(\overrightarrow i .\overrightarrow j \), \(\overrightarrow j .\overrightarrow k \), \(\overrightarrow k .\overrightarrow i \)

c) Tính tích vô hướng \(\overrightarrow a .\overrightarrow b \) theo toạ độ của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \).

Như vậy, điều kiện để 3 vectơ đồng phẳng trong không gian Oxyz là gì? Cách để chứng minh ba vectơ đồng phẳng như thế nào? chúng ta cùng tìm hiểu qua bài viết dưới đây.

I. Điều kiện để 3 vectơ đồng phằng trong không gian Oxyz

* Ở lớp 11, các em đã biết cách chứng minh 3 vectơ đồng phẳng như:

- Chứng minh các giá của ba vectơ cùng song song với một mặt phẳng.

- Dựa vào điều kiện để ba vectơ đồng phẳng: Nếu có m, n ∈ R sao cho:

+ Để phân tích một vectơ  theo ba vectơ không đồng phẳng, ta tìm các số m, n, p sao cho:

* Khi học tích có hướng ở toán lớp 12, để chứng minh 3 vectơ đồng phẳng thì:

II. Bài tập vận dụng tìm giá trị m để 3 vectơ đồng phẳng

* Bài tập 1: Trong không gian Oxyz cho ba vectơ:

Tìm x để 3 vectơ trên đồng phẳng.

* Bài tập 2: Trong không gian Oxyz, cho  và .

Tìm vectơ đơn vị đồng phẳng với   và tạo với  góc 450.

Giải hệ phương trình ta tìm được 2 vectơ thoả điều kiện bài toán:

* Bài tập 3: Tìm m để 3 vectơ sau không đồng phẳng.

Vậy với m = 1 hoặc m = 9 thì 3 vectơ  đồng phẳng

Suy ra, với m ≠ 1 và m ≠ 9 thì 3 vectơ  KHÔNG đồng phẳng

Hy vọng với bài viết điều kiện để 3 vectơ đồng phẳng trong không gian Oxyz toán lớp 12 ở trên đã giúp các em hiểu và nắm vững phần kiến thức này. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để Hay Học Hỏi ghi nhận và hỗ trợ, chúc các em học tốt.

Công thức tính Tích vô hướng của hai vecto trong không gian (cực hay)

Bài viết Công thức tính Tích vô hướng của hai vecto trong không gian với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Công thức tính Tích vô hướng của hai vecto trong không gian.

ĐỀ THI, GIÁO ÁN, GÓI THI ONLINE DÀNH CHO GIÁO VIÊN VÀ PHỤ HUYNH LỚP 12

Bộ giáo án, đề thi, bài giảng powerpoint, khóa học dành cho các thầy cô và học sinh lớp 12, đẩy đủ các bộ sách cánh diều, kết nối tri thức, chân trời sáng tạo tại https://tailieugiaovien.com.vn/ . Hỗ trợ zalo VietJack Official

phuong-phap-toa-do-trong-khong-gian.jsp

Giải bài tập lớp 12 sách mới các môn học

Bài tập vận dụng về vectơ trong không gian lớp 11 (có lời giải)

Có hình lăng trụ ABC.A’B’C’, chỉ ra các vecto bằng nhau và có điểm đầu và điểm cuối là đỉnh của hình lăng trụ.

Áp dụng tính chất của hình lăng trụ, ta sẽ có:

Cho hình chóp S.ABCD, đáy ABCD là hình bình hành. Hãy chứng minh:

$\overrightarrow{SA}+\overrightarrow{SC}=\overrightarrow{SB}+\overrightarrow{SD}$

Bài giải: Khi O là tâm của hình bình hành ABCD ta sẽ có:

Tứ diện ABCD. Trên AD có M vecto AM = 3. Vecto MD. N trên BC sao cho vecto NB= -3. Vecto NC. CM: vecto AB, DC, MN đồng phẳng

Cho hình hộp ABCD.A’B’C’D, hãy chứng minh:

Có tứ diện ABCD. Gọi G là trọng tâm tam giác ABC.

$\overrightarrow{DA}+\overrightarrow{DB}+\overrightarrow{DC}=3\overrightarrow{DG}$

Áp dụng quy tắc 3 điểm ta có

PAS VUIHOC – GIẢI PHÁP ÔN LUYỆN CÁ NHÂN HÓA

Khóa học online ĐẦU TIÊN VÀ DUY NHẤT:

⭐ Xây dựng lộ trình học từ mất gốc đến 27+

⭐ Chọn thầy cô, lớp, môn học theo sở thích

⭐ Tương tác trực tiếp hai chiều cùng thầy cô

⭐ Học đi học lại đến khi nào hiểu bài thì thôi

⭐ Rèn tips tricks giúp tăng tốc thời gian làm đề

⭐ Tặng full bộ tài liệu độc quyền trong quá trình học tập

Đăng ký học thử miễn phí ngay!!

Vecto trong không gian là gì?

Một đoạn thẳng có hướng được gọi là vecto trong không gian với kí hiệu $\overrightarrow{AB}$, điểm A là điểm đầu, điểm B là điểm cuối.

Cho hình bình hành ABCD thì ta có:

$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$

2.2. Quy tắc 3 điểm đối với phép cộng vecto

Khi có 3 điểm A, B, C bất kì thì:

$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{BC}$

Hoặc $\overrightarrow{AC}=\overrightarrow{BC}+\overrightarrow{AB}$

$\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}=\overrightarrow{AC'}$

Công thức tính Tích vô hướng của hai vecto trong không gian (cực hay)

Bài giảng: Các dạng bài tập hệ trục tọa độ trong không gian - Cô Nguyễn Phương Anh (Giáo viên VietJack)

Bài 1: Trong không gian với hệ trục tọa độ Oxyz, cho các vecto a→=(1;2;1),

b→=(3;-1;2), c→=(4; -1; -3),d→=(3; -3; -5),u→=(1;m;2),m∈R.

b) So sánh a→.(b→.c→) và (a→.b→ ) c→

c) Tính các góc (a→,b→ ), ( a→+b→,3a→- 2c→ )

c→ =(4; -1; -3)⇒2c→ =(8; -2; -6)⇒ a→ -2c→ =(-7;4;7)

⇒b→ (a→ -2c→ )=3.(-7)-1.4+2.7=-11

b) b→ .c→ =3.4+(-1).(-1)+2.(-3)=7⇒a→ .(b→ .c→ )=(7;14;7)

a→ .b→ =3⇒(a→ .b→ ) c→ =(12; -3; -9)

Vậy a→ .(b→ .c→ )≠(a→ .b→ ) c→

+ a→+ b→=(4;1;3),3a→- 2c→=(-5;8;9)

d) b→ +d→ =(6; -4; -3); u→ =(1;m;2)

u ⃗⊥(b→ +d ⃗ )⇔u→ .(b→ +d→ )=0⇔6-4m-6=0⇔m=0

(u→ ,a→ )=600⇔cos⁡(u→ ,a→ )=1/2

Bài 2: Trong không gian hệ tọa độ Oxyz, cho hai vecto a→,b→ sao cho (a→,b→ )=1200,

|a→ |=2; |b→ |=3. Tính |a→+ b→ | và |a→-2b→ |

Áp dụng công thức: a→ .b→ =|a→ |.|b→ |.cos⁡(a→ ,b→ )

Ta có: |a→ + b→ |2=(a→ + b→ )2=a→ 2+2a→ .b→ +b→ 2

=|a→ |2+|b→ |2+2|a→ |.|b→ |.cos⁡(a→ ,b→ )=4+9+2.2.3.((-1)/2)=7

|a→ -2b→ |2 =|a→ |2+4|b→ |2-4|a→ |.|b→ |.cos⁡(a→ ,b→ )=4+36-4.2.3.((-1)/2)=52

Bài 3: Trong không gian Oxyz, cho các điểm A(2; -1; 1), B(3; 5; 2), C(8; 4; 3), D(-2; 2m+1; -3)

a) Chứng minh tam giác ABC là tam giác vuông

b) Tìm m sao cho tam giác ABD vuông tại A

c) Tính số đo góc A của tam giác ABC

a) Ta có: AB→=(1;6;1); BC→=(5;-1;1)

b) AB→=(1;6;1); AD→=(-4;2m+2; -4)

Tam giác ABD vuông tại A ⇔AB→.AD→=0

Bài 1: Cho các vectơ u→(u1;u2;u3) và v→(v1;v2;v3), u→. v→=0 khi và chỉ khi:

Bài 2: Cho hai vectơ a→ và b→ tạo với nhau góc 600 và |a→| =2; |b→| =4. Khi đó |a→ + b→ | bằng:

|a→ + b→ |2=(a→ + b→ )2=|a→ |2+|b→ |2+2|a→ |.|b→ |.cos⁡(a→ + b→ )

Bài 3: Cho a→(-2;1;3), b→(1;2;m). Với giá trị nào của m để a→ vuông góc với b→ ?

a→ vuông góc với b→ khi và chỉ khi a→ . b→=0

Bài 4: Tính cosin của góc giữa hai vectơ a→ và b→ biết a→(8;4;1), b→(2;-2;1)

Bài 5: Cho tam giác ABC với A(-1;-2;4), B(-4;-2;0), C(3;-2;1). Khi đó số đo của góc BACˆ bằng:

Bài 6: Cho bốn điểm A(1;0;0), B(0;1;0), C(0;0;1), D(-2;1;-1). Khi đó số đo của góc giữa hai đường thẳng AB và CD là :

Gọi góc giữa 2 đường thẳng AB và CD là α

Bài 7: Trong không gian với hệ toạ độ Oxyz, cho hai vecto a→; b→. Trong các khẳng định sau, khẳng định nào đúng:

A. a→ .|b→ |=|a→ |.b→ với mọi a→ ; b→

B. ( a→ b→ )2=a→ 2 . b→ 2 với mọi a→ ; b→

C. |a→ . b→ | ≤|a→ |.|b→ | với mọi a→ ; b→

D. a→ . b→ =0 khi và chỉ khi a→ = 0→ hoặc b→ = 0→

d) a→ b→ =0 nhưng a→ ≠ 0→ hoặc b→ ≠ 0→

Bài 8: Trong không gian Oxyz, cho a→(-1;2;-3), b→(3;3;4), c→(5;0-1). Giá trị của a→ (b→ + c→ ) là:

⇒ a→ (b→ + c→ )=-1.8+2.3-3.3=-11

Bài 9: Cho 3 điểm A(2; 1; -3), B(–2; 2; –6), C(5; 0; –1). Tích AB→. AC→ bằng:

⇒ AB→ . AC→ =-4.3+1.(-1)-3.2=-19

Bài 10: Trong không gian với hệ tọa độ Oxyz, điều kiện để a→ vuông góc với b→ là gì ?

A. a→ . b→ =0   B. [ a→ , b→] = 0→

C. a→ + b→ = 0→   D. a→ - b→ = 0→

Bài 11: Cho hai vecto a→; b→thay đổi nhưng luôn thỏa mãn |a→|=5; |b→ |=3. Giá trị lớn nhất của |a→ -2 b→ | là:

Ta có: |a→ - 2 b→ |2 = ( a→ - 2 b→ )2 = | a→ |2 + 4| b→ |2 - 4| a→ |.| b→ |.cos⁡( a→ ; b→ )

| a→ -2 b→ | lớn nhất ⇔ | a→ - 2 b→ |2 lớn nhất ⇔cos⁡( a→ ; b→ )=0

Khi đó: | a→ - 2 b→ |2=| a→ |2+4| b→ |2=25+4.9=61

Bài 12: Trong không gian với hệ toạ độ Oxyz, cho ba vectơ a→(-1;1;0), b→(1;1;0), c→(1;1;1,). Trong các mệnh đề sau, mệnh đề nào sai ?

⇒ Hai vecto c→ ; b→ không vuông góc với nhau

Bài 13: Trong không gian với hệ toạ độ Oxyz, cho tam giác ABC có AB→=(-3;0;4), AC→=(5;-2;4). Độ dài trung tuyến AM là:

Ta có: AB=|AB→ |=5; AC=|AC→ |=√45

Ta có: BC2=AB2+AC2 - 2AB.AC.cos⁡BACˆ =68

Bài 14: Cho | a→ |=2; | b→ |=5, góc giữa hai vectơ a→ và b→ bằng (2π)/3, u→ = k a→ - b→; v→ = a→ + 2 b→. Để u→ vuông góc với v→ thì k bằng?

⇒ u→ . v→ =(k a→ - b→ )(a→ +2 b→ )=k a→ 2-2 b→ 2+(2k-1) a→ . b→

Ta có: a→ . b→ =| a→ |.| b→ |.cos⁡( a→ ; b→ )=2.5.cos⁡(2π/3)=-5

⇒ u→ . v→ =4k-2.25+(2k-1).(-5)=-6k-45

Giả thiết: u→ và v→ vuông góc với nhau ⇒ u→ . v→ =0

Bài 15: Trong không gian với hệ tọa độ Oxyz, cho a→=(x;2;1), b→ =(2;1;2), Tìm x biết cos( a→ , b→ )=2/3.

Bài 16: Trong không gian với hệ tọa độ Oxyz, cho A→ (-2;2;-1), B→ (-2;3;0), C→ (x;3;-1). Giá trị của x để tam giác ABC đều là:

AB→ =(0;1;1); AC→ =(x+2;1;0); BC→ =(x+2;0;-1)

Tam giác ABC đều ⇔ BACˆ= ABCˆ=600

Bài 17: Cho hai vecto a→; b→ tạo với nhau một góc 600. Biết độ dài của hai vecto đó lần lượt là 5 và 10. Độ dài của vecto hiệu a→ - b→ là:

Ta có: | a→ - b→ |2=( a→ - b→ )2=| a→ |2+| b→ |2-2| a→ |.| b→ |.cos⁡( a→ ; b→ )

Bài 18: Trong không gian với hệ tọa độ Oxyz,cho tam giác ABC với A(-4;3;5), B(-3;2;5) và C(5;-3;8). Tính cos⁡(AB→ ; BC→ ).

AB→ =(1; -1;0); BC→ =(8; -5;3)

Bài 19: Trong không gian với hệ toạ độ Oxyz, tam giác ABC có A(-1;-2;4), B(-4;-2;0), C(3;-2;1). Số đo của góc B là:

Bài 20: Trong không gian Oxyz, cho hai điểm A(x; y; z), B(m, n, p) thay đổi nhưng luôn thỏa mãn điều kiện x2+y2+z2=4; m2+n2+p2=9. Vecto AB→ có độ dài nhỏ nhất là:

Dấu bằng xảy ra khi O nằm ngoài đoạn AB.